Lesson 12 - FastAI
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)
path.ls()
lines = L()
with open(path/'train.txt') as f: lines += L(*f.readlines())
with open(path/'valid.txt') as f: lines += L(*f.readlines())
lines
This is what our data looks like right now
text = ' . '.join([l.strip() for l in lines]) #Reformating
text[:100]
tokens = text.split(' ') #Now lets tokenize it
tokens[:10]
vocab = L(*tokens).unique() #lets create our vocab
vocab
This will be our vocab:Lets also numericalize it.
word2idx = {w:i for i,w in enumerate(vocab)} #Dictionary of word:id
nums = L(word2idx[i] for i in tokens) #Numericalization
tokens[:10], nums
L((tokens[i:i+3], tokens[i+3]) for i in range(0,len(tokens)-4,3))
Tokens are created so that the 4th token is the label.
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0,len(nums)-4,3)) #Lets do the above, but this time using
seqs #numericalization form
bs = 64
cut = int(len(seqs) * 0.8) #80% training set, 20% valid set
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)
dls.one_batch()[0][:2]
Our Language Model in PyTorch
Below is our language model. As you see, we have created three layers:
- The embedding layer (
i_h, for input to hidden) - The linear layer to create the activations for the next word (
h_h, for hidden to hidden) - A final linear layer to predict the fourth word (
h_o, for hidden to output)
class LMModel1(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)#input
self.h_h = nn.Linear(n_hidden, n_hidden)#hidden
self.h_o = nn.Linear(n_hidden,vocab_sz)#output
def forward(self, x):
h = F.relu(self.h_h(self.i_h(x[:,0]))) #word 1
h = h + self.i_h(x[:,1]) #word 2
h = F.relu(self.h_h(h))
h = h + self.i_h(x[:,2]) #word 3
h = F.relu(self.h_h(h))
return self.h_o(h) #pred (word 4)
learn = Learner(dls, LMModel1(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
Awesome we created our first NLP model!
n,counts = 0,torch.zeros(len(vocab))
for x,y in dls.valid:
n += y.shape[0]
for i in range_of(vocab): counts[i] += (y==i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n
Our acc would have been .15 had we used an naive model
class LMModel2(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
def forward(self, x):
h = 0
for i in range(3): #lets use a forloop to create layers
h = h + self.i_h(x[:,i])
h = F.relu(self.h_h(h))
return self.h_o(h)
Notice that here h is set to 0 after every batch
learn = Learner(dls, LMModel2(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy)
learn.fit_one_cycle(4, 1e-3)
Roughly the same as we expected. However, what we have created this time is actually an RNN!
class LMModel3(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
for i in range(3):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
out = self.h_o(self.h)
self.h = self.h.detach() #detach throws away the stored gradients - However, the activations are still stored
return out
#Start of each epoch, we should reset out h
def reset(self): self.h = 0
m = len(seqs)//bs
m,bs,len(seqs)
def group_chunks(ds, bs):
m = len(ds) // bs
new_ds = L()
for i in range(m): new_ds += L(ds[i + m*j] for j in range(bs))
return new_ds
group_chunks(seqs, bs)[1:4]
seqs[m,m*2,m*3]
Lets recreate our dataloader using our improved minibatch format
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)
learn = Learner(dls, LMModel3(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy, cbs=ModelResetter) #This will call our reset function
learn.fit_one_cycle(10, 3e-3)
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0,len(nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
#dataloader
dls = DataLoaders.from_dsets(group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)
seqs[0]
[vocab[s] for s in seqs[0]]
class LMModel4(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
outs = [] #list of output
for i in range(sl):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
outs.append(self.h_o(self.h)) #append
self.h = self.h.detach()
return torch.stack(outs, dim=1) #stack of outputs
def reset(self): self.h = 0
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))
learn = Learner(dls, LMModel4(len(vocab), 64), loss_func=loss_func,
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
Better than before!
class LMModel5(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = torch.zeros(n_layers, bs, n_hidden)
#How many layer to stack
self.rnn = nn.RNN(n_hidden, n_hidden, n_layers, batch_first=True) #This is doing what our previous model did:
#Looping of the layers
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h) #Notice that we can do the loop by calling our RNN
self.h = h.detach()
return self.h_o(res)
def reset(self): self.h.zero_()
learn = Learner(dls, LMModel5(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 3e-3)
Our model did worse. Does that mean our model is bad? No, what most likley happened here is that our gradient has either exploded or disappeared.
class LSTMCell(Module):
def __init__(self, ni, nh):
self.forget_gate = nn.Linear(ni + nh, nh)
self.input_gate = nn.Linear(ni + nh, nh)
self.cell_gate = nn.Linear(ni + nh, nh)
self.output_gate = nn.Linear(ni + nh, nh)
def forward(self, input, state):
h,c = state
h = torch.cat([h, input], dim=1)
forget = torch.sigmoid(self.forget_gate(h))
c = c * forget
inp = torch.sigmoid(self.input_gate(h))
cell = torch.tanh(self.cell_gate(h))
c = c + inp * cell
out = torch.sigmoid(self.output_gate(h))
h = out * torch.tanh(c)
return h, (h,c)
We can refactor the above code
class LSTMCell(Module):
def __init__(self, ni, nh):
self.ih = nn.Linear(ni,4*nh)
self.hh = nn.Linear(nh,4*nh)
def forward(self, input, state):
h,c = state
# One big multiplication for all the gates is better than 4 smaller ones
gates = (self.ih(input) + self.hh(h)).chunk(4, 1)
ingate,forgetgate,outgate = map(torch.sigmoid, gates[:3])
cellgate = gates[3].tanh()
c = (forgetgate*c) + (ingate*cellgate)
h = outgate * c.tanh()
return h, (h,c)
t = torch.arange(0,10); t
t.chunk(2)
class LMModel6(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)] #more hidden state layers because LSTM has more layers
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True) #Replace our RNN to LSTM
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h)
self.h = [h_.detach() for h_ in h]
return self.h_o(res)
def reset(self):
for h in self.h: h.zero_()
learn = Learner(dls, LMModel6(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=ModelResetter)
learn.fit_one_cycle(15, 1e-2)
Our model is doing much better now
Regularizing an LSTM
Will be using some regularization technique to improve our model's gradients, particularly Dropout. What dropout does is that it randomly drops some neurons each minibatch: This forces the model to become more robust by making it able to produce the correct prediction even with less neurons available.
class Dropout(Module):
def __init__(self, p):
self.p = p #probility that activation gets deleted
def forward(self, x):
if not self.training: #NO DROPOUT DURING TESTING (Only occurs during training)
return x
mask = x.new(*x.shape).bernoulli_(1-self.p) #1's and 0's where 1-p is the prob that we get a 1
return x * mask.div_(1-self.p)
Activation regularization (AR) and temporal activation regularization (TAR) are two regularization methods very similar to weight decay, which we have discussed before.
For activation regularization, it's the final activations produced by the LSTM that we will try to make as small as possible, instead of the weights.
loss += alpha * activations.pow(2).mean()
Temporal activation regularization is there to encourage that behavior by adding a penalty to the loss to make the difference between two consecutive activations as small as possible:
loss += beta * (activations[:,1:] - activations[:,:-1]).pow(2).mean()
class LMModel7(Module):
def __init__(self, vocab_sz, n_hidden, n_layers, p):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.drop = nn.Dropout(p) #Dropout
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h_o.weight = self.i_h.weight #Hidden-to-output weights are set identical to input-to-hidden
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
raw,h = self.rnn(self.i_h(x), self.h)
out = self.drop(raw)
self.h = [h_.detach() for h_ in h]
return self.h_o(out),raw,out
def reset(self):
for h in self.h: h.zero_()
Notice that Hidden-to-output and input-to-hidden are linked by the same parameters
learn = Learner(dls, LMModel7(len(vocab), 64, 2, 0.5),
loss_func=CrossEntropyLossFlat(), metrics=accuracy,
cbs=[ModelResetter, RNNRegularizer(alpha=2, beta=1)]) #Although we didn't create our regularizer, we can still
#pass it via cbs.
learn = TextLearner(dls, LMModel7(len(vocab), 64, 2, 0.4),
loss_func=CrossEntropyLossFlat(), metrics=accuracy)
Calling TextLearner will automatically add ModelResetter, RNNRegularizer(alpha=2, beta=1) for us
learn.fit_one_cycle(15, 1e-2, wd=0.1)
- If the dataset for your project is so big and complicated that working with it takes a significant amount of time, what should you do?
Create a simple dataset that allow for quick and easy prototyping. - Why do we concatenate the documents in our dataset before creating a language model?
This allows us to easily split up data into batches. - To use a standard fully connected network to predict the fourth word given the previous three words, what two tweaks do we need to make to our model?
Use same weight matrix for the three layers.
Use the first word’s embeddings as activations to pass to linear layer, add the second word’s embeddings to the first layer’s output activations, and continues for rest of words. - How can we share a weight matrix across multiple layers in PyTorch?
Define one layer in the PyTorch model class and use it multiple times in the forward pass. Write a module that predicts the third word given the previous two words of a sentence, without peeking.
class LMModel1(Module): def __init__(self, vocab_sz, n_hidden): self.i_h = nn.Embedding(vocab_sz, n_hidden) self.h_h = nn.Linear(n_hidden, n_hidden) self.h_o = nn.Linear(n_hidden,vocab_sz) def forward(self, x): h = 0 for i in range(3): h = h + self.i_h(x[:,i]) h = F.relu(self.h_h(h)) return self.h_o(h)
- What is a recurrent neural network?
A refactoring of a multi-layer neural network as a loop. - What is "hidden state"?
Hidden state's are the activations updated after each RNN step. - What is the equivalent of hidden state in
LMModel1?
h - To maintain the state in an RNN, why is it important to pass the text to the model in order?
Because state is maintained over all batches, so order matters. - What is an "unrolled" representation of an RNN?
A representation without loops. - Why can maintaining the hidden state in an RNN lead to memory and performance problems? How do we fix this problem?
Backpropagation would cause it to calculate the gradients of all the past calls. This can be avoided using detach(). - What is "BPTT"?
Calculating backpropagation only for the given batch (detach()). - Write code to print out the first few batches of the validation set, including converting the token IDs back into English strings, as we showed for batches of IMDb data in <
>.</strong> </li>[vocab[s] for s in dls.one_batch[0]]
- What does the
ModelResettercallback do? Why do we need it?
It calls our reset method, which resets our hidden state before every epoch.- What are the downsides of predicting just one output word for each three input words?
There is a lot of extra information for training the model that is not being used.- Why do we need a custom loss function for
LMModel4?
We have a stacked output, which we need to flatten as CrossEntropyLoss expects flattened tensors.- Why is the training of
LMModel4unstable?
Because this network is very deep it leads gradient to explode or disappear- In the unrolled representation, we can see that a recurrent neural network actually has many layers. So why do we need to stack RNNs to get better results?
Because only one weight matrix is really being used. We can fix this by stacking.- Draw a representation of a stacked (multilayer) RNN.
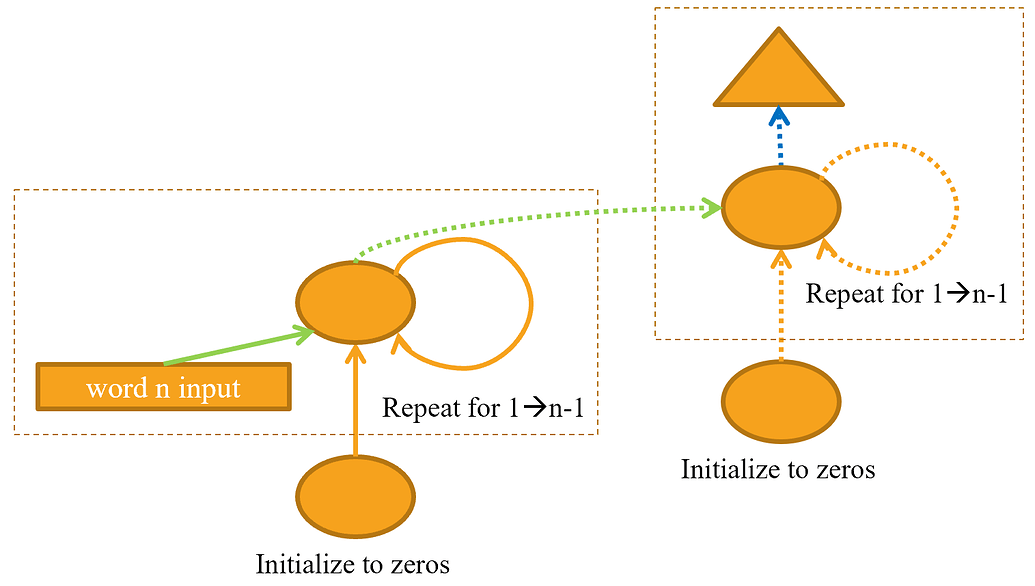
- Why should we get better results in an RNN if we call
detachless often? Why might this not happen in practice with a simple RNN?- Why can a deep network result in very large or very small activations? Why does this matter?
Numbers that are slightly large or small can lead to the explosion or disappearance of the number after repeated multiplications. In deep networks, we have repeated matrix multiplications, so this is a big problem.- In a computer's floating-point representation of numbers, which numbers are the most precise?
Small numbers (Not too close to 0 however)- Why do vanishing gradients prevent training?
No gradients mean no change in weights- Why does it help to have two hidden states in the LSTM architecture? What is the purpose of each one?
One state remembers what happened earlier in the sentence, and the other predicts the next token.- What are these two states called in an LSTM?
Cell state (long short-term memory)
Hidden state (prediction)- What is tanh, and how is it related to sigmoid?
A sigmoid function rescaled to the range of -1 to 1- What is the purpose of this code in
LSTMCell:h = torch.cat([h, input], dim=1)
Joins the hidden state and the new input.- What does
chunkdo in PyTorch?
Splits tensor in equal sizes.- Study the refactored version of
LSTMCellcarefully to ensure you understand how and why it does the same thing as the non-refactored version.- Why can we use a higher learning rate for
LMModel6?
Because now that we are using an LSTM, we have a partial solution to exploding/vanishing gradients.- What are the three regularization techniques used in an AWD-LSTM model?
Dropout
Activation regularization
Temporal activation regularization- What is "dropout"?
Random removal of neurons- Why do we scale the weights with dropout? Is this applied during training, inference, or both?
The scale changes if we sum up activations, so to correct the scale, a division by (1-p) is applied. We applied this only during training, but can be done both ways.- What is the purpose of this line from
Dropout:if not self.training: return x
Prevents the usage of dropout during testing.- Experiment with
bernoulli_to understand how it works.- How do you set your model in training mode in PyTorch? In evaluation mode?
Module.train(), Module.eval()- Write the equation for activation regularization (in math or code, as you prefer). How is it different from weight decay?
It's different because here we are not decreasing the weights, rather the activationsloss += alpha * activations.pow(2).mean()
- Write the equation for temporal activation regularization (in math or code, as you prefer). Why wouldn't we use this for computer vision problems?
This focuses on making the activations of consecutive tokens to be similar:loss += beta * (activations[:,1:] - activations[:,:-1]).pow(2).mean()
- What is "weight tying" in a language model?
</ol> </div> </div> </div>
Where weights of hidden-to-output layer is the same as input-to-hidden.- In
LMModel2, why canforwardstart withh=0? Why don't we need to sayh=torch.zeros(...)? - Write the code for an LSTM from scratch (you may refer to <
>).</li> - Search the internet for the GRU architecture and implement it from scratch, and try training a model. See if you can get results similar to those we saw in this chapter. Compare you results to the results of PyTorch's built in
GRUmodule.- Take a look at the source code for AWD-LSTM in fastai, and try to map each of the lines of code to the concepts shown in this chapter.
</ol> </div> </div> </div> </div> - Search the internet for the GRU architecture and implement it from scratch, and try training a model. See if you can get results similar to those we saw in this chapter. Compare you results to the results of PyTorch's built in
- What does the